610
Tiempo medio (T½)
, es un parámetro farmacocinético del
que muchas veces se habla. Es el tiempo (normalmente en
horas) para que la concentración del fármaco se reduzca
a la mitad. La utilidad de conocerlo permite saber cuándo
se alcanza el estado estacionario del fármaco (aquel
momento en que, pese a las sucesivas dosis, la concen-
tración plasmática sigue aumentando y siempre se mueve
en un rango), así como también, predecir cuándo se elimi-
naría el fármaco del organismo (4,7). Para ambos escena-
rios, 5 o 6 veces la vida media del fármaco será el tiempo
necesario para conseguir cualquiera de las dos situaciones.
(Nota: con este criterio, el estado estacionario se alcanza si
la frecuencia de administración es igual al T½. Ejemplo: en
niños, vancomicina tiene T½ = 6h, y la posología es 15mg/
kg cada 6 h. El tiempo para alcanzar el estado estacionario
será 5*6h = 30h. Por otro lado, fármacos con corta vida
(ejemplo 1h), cuya frecuencia de administración es cada
12 horas, no alcanzarían nunca el estado estacionario. En
ese caso, a las 5*1h=5h ya no quedaría una concentración
detectable en sangre).
Por último, la
excreción del fármaco
frecuentemente
se relaciona con la función renal del paciente. Muchos
fármacos se eliminan por filtración glomerular por lo
tanto, aquellas fórmulas basadas en el
clearance
de crea-
tinina plasmática para estimar la velocidad de filtra-
ción glomerular, como la fórmula de Cockroft-Gault,
Modification of Diet in Renal Disease (MDRD)
, o Schwartz
(usada en pediatría) ayudarían a evaluar la necesidad de
ajustar la dosis. (26)
Con los datos de concentración plasmática versus tiempo de
una dosis (Figura 1), la farmacocinética se puede estudiar
utilizando modelos que simplifican los datos. De allí provienen
fórmulas matemáticas con las que se pueden calcular poste-
riormente los parámetros farmacocinéticos (4).
Normalmente se emplean modelos compartimentales para
favorecer la comprensión de los cambios en el ADME. En
la Figura 3 se esquematizan los modelos más frecuentes.
Así, el comportamiento de muchos fármacos se puede
ajustar a modelos de 1 compartimento, en el que la dosis
administrada alcanza rápidamente el equilibrio de distri-
bución, tan rápida que es imposible caracterizarla. Ejem-
plos clásicos de este comportamiento son los fármacos
hidrofílicos, como
β
-lactámicos o aminoglicósidos. En
cambio, otros fármacos pueden caracterizarse por modelos
de 2 compartimentos. En ellos, el equilibrio de distribu-
ción es más lento, y se requiere esperar alcanzarlo antes
para interpretar las variaciones cinéticas. La mayoría de
los fármacos liposolubles tendrían este modelo. Incluso de
más de 2 compartimentos (4,7,17).
Es posible estudiar el comportamiento de un fármaco de
2 compartimentos con el modelo de 1 compartimento por
la simplicidad en el manejo de los datos, pero es necesario
considerar la imprecisión de ese ajuste.
Por último, es importante conocer
el tipo de cinética
involucrada.
Algunos fármacos tienen una velocidad de
eliminación lineal (también llamada cinética orden 1),
y otros, una velocidad no lineal (cinética de orden cero)
(4,7,17).
Cuando la cinética es lineal, la concentración plasmática
cambiaría linealmente con la dosis; la eliminación es cons-
tante y es una fracción del fármaco por unidad de tiempo.
Así, el ABC, Cl, Vd, y t½ se mantienen constantes, por lo
que cambios en la dosis no deberían generar cambios en
esos parámetros.
En el caso que la cinética es no - lineal, existe una variación
que no es proporcional a la dosis administrada. En esos
fármacos, los parámetros farmacocinéticos son fluctuantes
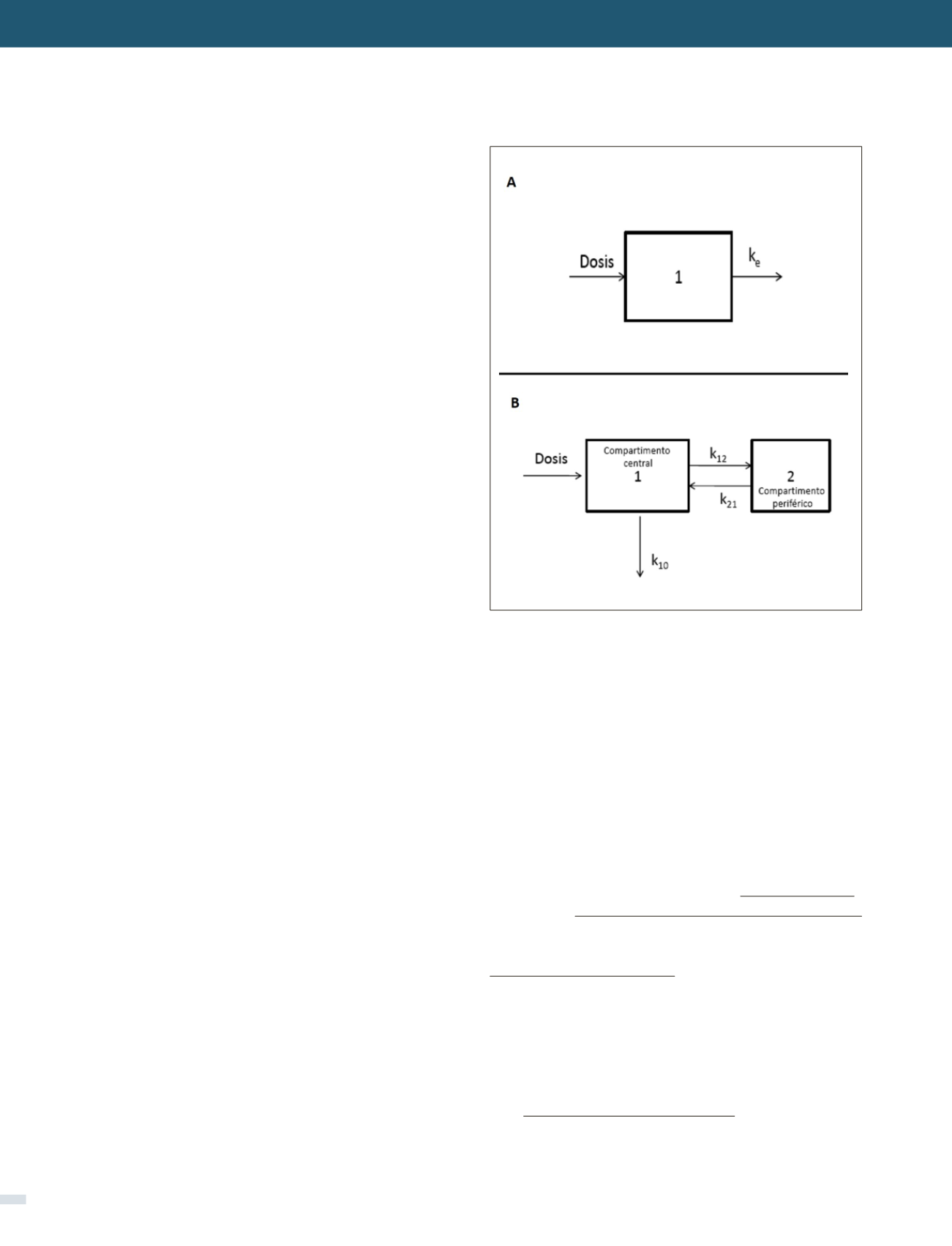
FIGURA 3. ESQUEMA DE MODELOS COMPARTIMENTALES
A: modelo de 1 compartimento. La dosis se distribuye rápidamente en el
compartimento central (1), alcanzando el equilibrio de distribución inme-
diatamente.
B: modelo de 2 compartimentos. La dosis se distribuye primero en el
compartimento central (1) y luego en el compartimento periférico (2).
La distribución no es instantánea, demora un tiempo hasta alcanzar el
equilibrio.
[REV. MED. CLIN. CONDES - 2016; 27(5) 605-614]








